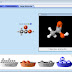
A descrição do movimento de um corpo faz-se indicando a sua localização em cada instante, sendo necessário medir o tempo e posições em relação a um ponto de referência. Para simplificar o problema e eliminar efeitos pouco relevantes para o que pretendemos descrever, o corpo pode ser representado por um ponto. [Sequências 1 e 2 na animação abaixo]
À medida que o corpo se move descreve uma trajectória. Na nossa descrição, o que pretendemos é indicar onde ele se encontra a cada momento. Assim a trajectória corresponde a uma função matemática que nos fornece para cada instante de tempo a posição do corpo. Em geral uma trajectória corresponde a uma sequência de conjuntos de quatro números (x, y, z, t). Cada um desses conjuntos inclui o instante de observação t e as três coordenadas x, y, z, da posição do objecto nesse instante. [Sequências 1 a 4 na animação abaixo]
Para evitar incompreensões desnecessárias é necessário saber distinguir claramente os conceitos de distância percorrida e de deslocamento. A próxima animação ajuda à clarificação.
[Sequência 1 na animação abaixo] Para indicar que a posição do corpo a cada instante é relativa ao ponto de referência O, costuma-se representá-la por um vector de posição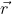 
, em que as componentes do vector são as coordenadas do objecto. A trajectória do corpo pode então ser representada por uma função r(t) que para cada instante t fornece o vector de posição.
[Sequência 2 na animação abaixo] A velocidade média corresponde ao vector 
A velocidade é, portanto, uma grandeza vectorial, ou seja, tem uma direcção e um sentido associados. Para descrever o movimento do corpo temos de indicar o seu módulo, a direcção e sentido do movimento.
[Sequência 3 na animação abaixo] A velocidade instantânea no instante t corresponde ao vector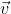 
(tangente à trajectória) quando t2 e t1 são instantes de tempo infinitamente próximos [Sequência 4 na animação abaixo]: 
(esta expressão pode agora parecer complicada para muitos, mas quando terminarem a Matemática de 11º verão que é fácil)
Quando o corpo se deslocar segundo uma linha recta, tudo se simplifica pois basta-nos uma medição para saber onde ele se encontra. Trata-se de um movimento rectilíneo. Neste caso a posição, definida por uma única grandeza x, é uma função do tempo: x(t).
Para um movimento rectilíneo o módulo v da velocidade define-se por 
. Note-se que a alteração de sentido do movimento se traduz numa alteração de sinal da velocidade.
Ao longo da sua trajectória o corpo pode deslocar-se mais ou menos depressa. Quer isto dizer que distâncias equivalentes podem ser percorridas em menos ou mais tempo.
[Sequência 1 na animação abaixo] Tal como no caso da posição, também a velocidade é uma função do tempo. Para o movimento rectilíneo, a direcção não muda, mas pode mudar o sentido ou o módulo. O exemplo de movimento mais simples corresponde ao caso em que a velocidade do corpo é constante. Constante significa aqui que a velocidade não se altera em módulo, direcção ou sentido, ou seja, que o movimento é rectilíneo. Designa-se por isso de rectilíneo uniforme.
[Sequência 2 na animação abaixo] Quando a velocidade não é constante o movimento torna-se mais complexo. O caso mais simples que podemos encontrar nessas condições ocorre quando temos um movimento rectilíneo em que a velocidade se altera de forma constante e designa-se por uniformemente variado (se o módulo da velocidade aumentar é acelerado e se diminuir é retardado).
Essa taxa de variação designa-se por aceleração e é, tal como a velocidade, uma grandeza vectorial, isto é, tem uma direcção e sentido (a direcção e sentido da alteração da velocidade) e um módulo. Matematicamente o módulo a da aceleração define-se então por 
. Note-se que o aumento ou diminuição da velocidade se traduz numa alteração de sinal da aceleração (positivo para um aumento de velocidade e negativo para uma diminuição).
O conteúdo deste post foi adaptado de [1] e [2].
Brevemente seguir-se-ão outros artigos dando continuidade ao tema.
Al-Khalili fala-nos da possibilidade da existência de universos paralelos, em que existirão diferentes versões de cada um de nós, e de que, afinal, o espaço vazio pode não o ser. 
Ano Internacional da Astronomia 2009 - E Agora Eu Sou Galileu
![distillation-i_final_2-220k%5B(003749)17-10-35%5D[1]](http://lh4.ggpht.com/_aTH7N3_trjA/SsINVXlIxWI/AAAAAAAABYM/-amBMHQD7DM/s1600-h/distillation-i_final_2-220k%5B%28003749%2917-10-35%5D%5B1%5D%5B2%5D.jpg "distillation-i_final_2-220k%5B(003749)17-10-35%5D[1]")
![image[28]](http://lh4.ggpht.com/_aTH7N3_trjA/SsEWpVxpotI/AAAAAAAABXs/TC8uWhkxnvg/s1600-h/image%5B28%5D%5B4%5D.jpg "image[28]")
![image[29]](http://lh3.ggpht.com/_aTH7N3_trjA/SsEWsSFQ4AI/AAAAAAAABX0/22tzmwtkzLc/s1600-h/image%5B29%5D%5B4%5D.jpg "image[29]")
![image[25]](http://lh5.ggpht.com/_aTH7N3_trjA/SsEWvYumM7I/AAAAAAAABX8/u2ObDbFHX-E/s1600-h/image%5B25%5D%5B5%5D.jpg "image[25]")
![image[26]](http://lh5.ggpht.com/_aTH7N3_trjA/SsEWxdH-OuI/AAAAAAAABYE/7zckqkJo_nw/s1600-h/image%5B26%5D%5B5%5D.jpg "image[26]")
