
Os portugueses não são conhecidos por serem pontuais, bem pelo contrário. Esta falta de pontualidade é frequentemente apontada por estrangeiros como um dos nossos grandes defeitos.
Esta incapacidade de chegar a horas a um encontro terá algo a ver com a dificuldade na matemática que alguns acreditam ser genética (eu não!) e que parece fazer parte do nosso fado?
Quantos não ouvimos já dizer, “Deixa filho, eu também não era bom (ou boa) com números.” ?
Será que alguns de nós nunca sabem às quantas andam, e raramente são pontuais porque a matemática lhes faz confusão? Ou será só falta de respeito pelo outro? Ou ambas?
Se, ao olhar para o relógio, vir um conjunto de símbolos ininteligíveis, então é provável que seja português (atenção, também pode ser brasileiro).
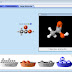
Quem aceita o desafio de explicar as representações matemáticas que estão presentes na imagem? Confesso a minha ignorância quanto a algumas delas, mas ao pesquisar já aprendi umas quantas coisas.
Vou dar uma ajuda. O 3! não é um 3 para ser lido enfaticamente, mas sim o factorial de 3, que significa 3x2x1. Esta era fácil.














12 comentários:
Um exemplo da excelência dos nossos alunos na Matemática: pagamento na caixa do supermercado. Valor: 16,35 euros. O cliente diz: só tenho 20 euros mas posso dar-lhe 1,35 euros. A funcionária da caixa olha para o dinheiro entregue pelo cliente, olha para o computador, olha novamente para o cliente. Após alguns (longos)segundos diz: Para quê? Cliente: para me dar 5 euros. De novo o olhar de perplexidade e nova espreitadela ao ecrã do computador. Cliente: Deixe estar!
Assim vai o país...
Que relógio tão esquisito. É uma coisa que eu não gosto é de chegar atrasado nem de fazer os outros esperar. Gosto de ser pontual. :P
E deixa-me adivinhar Patrícia, a funcionária era uma jovem, certo?
@ Estevão,
e não arriscas descodificar uma ou duas "esquisitices"?
Eu como sei ver as horas com os ponteiros é facil. Já vou ver isso.
Rui:
Como explicar o caso das pessoas que são pontuais mas não são grande espingarda a matemática? Há muitas pessoas portuguesas (e, claro, muitas não portugueses) nessa categoria.
E as pessoas que são boas ou excelentes a matemática e não são pontuais? Há muitas pessoas portuguesas (e, claro, muitas não portugueses) nessa categoria.
Eu não percebo nada de matemática (mas duvido que isso tenha uma relação relevante com o facto de ser português).
Todavia, desconfio que a resposta a essas perguntas - que cabe à Psicologia, à Sociologia e eventualmente à Biologia - é muito mais difícil que a Matemática. Seja um português ou um estrangeiro a tentar encontrá-la.
Cumprimentos!
Sim Rui, esqueci-me de referir que a funcionária era uma jovem.
Não podemos fazer deste exemplo uma regra, mas os professores que têm que utilizar a Matemática na aula, sejam eles da disciplina ou não, sabem que esta é uma realidade cada vez mais frequente, muito diferente dos resultados nacionais das provas de aferição e dos exames.
Bom galera!
eu posso desvendar algumas "esquisitices":
o que seria o 2 é o somatório(a soma) das potências não positivas(0,-1,-2,-3,...) de 2: 1+0,5 +0,25+0,125+...
o que seria o 10, é o Binomial de Newton(imaginem um parênteses só):
(p) = p!/(p-n)!x(n!)
(n)
no caso:
(5)=5!/3!x2!=5x4x3x2x1/(3x2x1x2x1)
(2)
ou seja, 10.
o 12 é a raiz cúbica de 1728, 1728=12x12x12=12³
O resto não tenho certeza...
O 8 deve ter algo a ver com binário...
O 5 só faz sentido se fi(o rabisco)=1,6180339887498948482045868343656 (da calculadora do Windows), ou seja, alguma constante qualquer...
O resto não sei...
Abraços!
Greyhawke
PS: Sou brasuca com orgulho... xD
Olá Greyhawke,
obrigado pelo seu excelente contributo.
Sei mais algumas, mas não queria ser eu a dizer ;)
Cumprimentos para esse lado do Atlântico.
O rabisco que o Greyhawke fala é o "número de ouro" que é igual a (1+raiz de 5)/2.
O 8 penso que é código de Morse ( logo verifico e já digo)
O 9 é 21 na base 4 . Ora 21 na base 4 é igual a 2x4^1+1x4^0, ou seja 9 na base 10.
Os outros não sei mas vou procurar saber
Olá Fernanda e obrigado pelo seu contributo.
Foi mais uma óptima achega para a descodificação desta simbologia.
Aqui fica outra solução:
a simbologia representada na posição 3 é o símbolo unicode em XML (linguagem informática / programação, utilizada, por exemplo, para construir a página que estão a ler) para o número 3.
Um bom dia.
Nota: os 3 que surgem no comentário anterior foram escritos por mim utilizando a referida simbologia e, após publicar o comentário, foram imediatamente interpretados como 3 e os símbolos desapareceram.
-O 7 é 6.999999999(...). É uma dízima infinita de período 9, que arredonda para 7, e que pode ser considerada 7 já que continua indefinidamente.
-Se bola preta é 1, e bola branca 0, o 8 está escrito em código binário.
Enviar um comentário
1) Identifique-se.
2) Seja respeitoso e cordial.
3) São bem-vindas críticas construtivas e correcções.
4) Leia primeiro os comentários anteriores.